 |
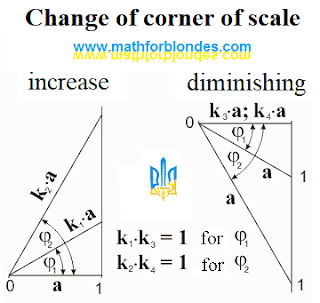
| Change of corner of scale |
An increase and diminishing of scale in the identical amount of one times correspond to one value of corner of scale. On this property of corners of scale trigonometric dependences are based in a rectangular triangle.
From the point of view of mathematical result does not matter, as a change of quantity is described in relation to unit of measurement. A variable quantity at permanent unit of measurement and variable unit of measurement at a permanent quantity will give the identical value of corner of scale.
In a general view the change of scale of quantity can be presented as a turn of unit of measurement on the size of corner of scale. An increase or diminishing of scale depends on that, what position of unit of measurement is taken for basis at comparison and from the type of projection. The increase of scale can be presented as a radial projection on a number ray, perpendicular to the unit of measurement taken for basis at comparison. Diminishing of scale can be presented as a perpendicular projection of the compared unit of measurement on the unit of measurement taken for basis.
 |
| Turn of unit of measurement on the corner of scale |
Expl for blondes: A boring entry is farther closed and interesting begins are trigonometric dependences of corner of scale. More interesting things on the page "New Math".
No comments:
Post a Comment