Modulus of sine

Me it was asked to show method to simplify trigonometric expression, containing the sum of sine and modulus of sine of corner, knowing that corner alpha is finished in 4 fourths. This expression looks so:

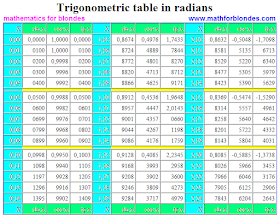
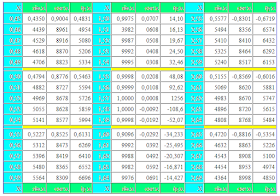
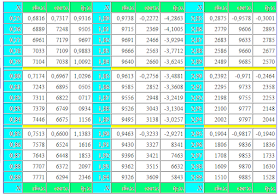
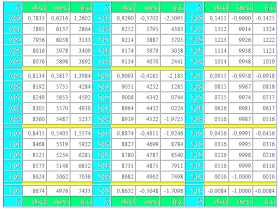
|sinA|+sinA

At once I will say honestly, that I a concept do not have, as such expressions are simplified. But about the module of sine I can tell and that will turn out in the total, then. All of you know well, that a sine, as well as all trigonometric functions, can take on positive and negative values. So, sine in the Chinese sticks, that in mathematics read as a "module of sine of corner A", can not have negative values, only positive. When mathematicians are fastidious to touch to the negative numbers, they apply these chopsticks (or modulus of number), as condom at sex, that to be not infected by minus. They rescue the life these, as all numbers in the module from negative grow into positive.


Well now a bit about sign life of sine of corner of А. Sine - it for us upwards and downward on an axis Y-mill from unit to minus units. When corner A from 0 to 180 degrees take on values, all sines of these corners are positive. In this case the chopsticks of the module are the superfluous measure of caution and they can be cast aside. In this range of values of corner A our expression will assume an air:

|sinA|+sinA = sinA+sinA = 2sinA (0 < A < 180)

If value of corner A to increase farther, from 180 to 360 degrees, values of sines of these corners will be negative, id est with a sign " minus". In this case the module begins to play the rock role the fate of our mathematical expression. The value of sine with the module remains positive, and the value of sine without the module becomes negative, as well as it is fixed to all decent sines. What will we get, if from a number we will take away a such is exact number? Correctly, zero. Our expression dies out, as dinosaurs. By the way, if all people always will use condoms during sex, humanity here will die out fully. Effect of the modulus. We will look, that takes place with our expression in this case:

|sinA|+sinA = sinA-sinA = 0 (180 < A < 360)

Application of formulas of bringing trigonometric functions over will give an exactly such result. Thus the module compels us to cast aside in garbage all signs minus, got as a result of transformations.

At corners 0, 180, 360 et cetera degrees our expression will equal a zero, as a zero the values of sine of these corners are equal to.

As all of it it is correct to write down in complete accordance with the rules of mathematical bureaucracy, I do not know. But sense of what be going on, I hope, clear you and you without effort will design this expression in the best kind.

Trigonometric table in radians

This trigonometric table is made for the values of corners in radians. Radians are here given as decimal fractions within two signs after a comma. Value of sine, cosine and tangent given within four signs after a comma. It is such small trigonometric table in radians. You can see the picture Degree-Radian Conversion at the end of the page.

Table of trigonometric values in degrees:
sin cos
tan cot

In this trigonometric table the value of corner in radians closes on a 3,15 radian, that corresponds hardly anymore 180 degrees in the degree measure of corners. Here you will not find the value of tangent, equal to unit, value of sine, equal to unit and value of cosine, equal to the zero. In the radian measure of corners to get these values unassisted number of Pi it is impossible. And as a self number of Pi is an endless shot not having the exact meaning, expediency of goniometry in radians is very doubtful. Radians - it, put it mildly, strange unit of measurement.

Values of corner in radians are in blue columns mark the letter of "X". In three columns the values of sin x are given on the right, cos x and tg x for corners in radians. Value of cotangent, secant and cosecant to the table not driven, as these trigonometric functions are reverse shots to driven to the table. For the receipt of values of ctg x, sec x and cosec x in radians, it is needed to divide unit into a tangent, cosine or sine of corresponding corner in radians.

Degree-Radian Conversion

Trigonometric table tangent cotangent in degrees

Trigonometric table tangent cotangent in degrees - it is the four-valued table of tangents and cotangents in degrees within one minute. A few examples are made at the beginning, as to use this table. For comfort in a table additional navigation elements are plugged with pointing by the name of the names of functions and values of minutes column-wise for every function. Value of degrees and minutes for every trigonometric function distinguished by different colors: for tangents - green, for cotangents - blue. Connotations for minutes are distinguished by yellow.

A trigonometric table for tangents and cotangents consists of two parts. The first part includes tangents from 0 to 75 degrees and cotangents from 15 to 90 degrees. Before to use this table, it is recommended on present examples to find the values of tangents and cotangents on a table and compare results. If all turned out correctly for you, means you can consider itself an experience user of table.







At the use it is necessary to remember this table, that additional values one, two and three minutes for a tangent have a sign plus and at addition added and at deduction subtracted, for a cotangent they have a sign minus and at addition subtracted, and at deduction added. For verification compare the got result to the values of the same name trigonometric functions in the alongside located cells.

The second part of trigonometric table includes tangents from 75 to 90 degrees and cotangents from 0 to 15 degrees. To use this table some simpler, than by the first part.






For a tangent 90 degrees and cotangent 0 degrees a value is not certain. It is so accepted to consider because task on dividing by a zero mathematicians until now so not succeeded to decide.

If you need a trigonometric table of sines and cosines, then she can be found on a separate page.