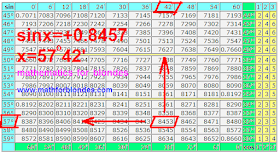
We must find a sine x with minus, a value is equal -0.8453
sin x = -0.8453
On the table of sines we find the value of corner in degrees and minutes for x, equal +0.8453. This corner is in limits from 0 to 90 degrees and equal 54 degrees 42 minutes.
sin a = +0.8453
a = 57 degrees 42 minutes
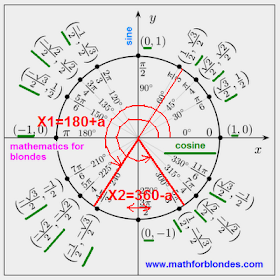
Farther we look a trigonometric circle and find a corner a. The positive values of sine are located in the overhead half of circle, negative values will be situated in the underbody of trigonometric circle.
One value of sine always has two values of corner. We will find these corners for the negative value of sine.
The first corner we will get, if to the corner a we will add 180 degrees. The second corner we will get, if from 360 degrees we will take away a corner a.
x1 = 180 degrees + a
x1 = 180 degrees + 57 degrees 42 minutes
x1 = (180 + 57) degrees 42 minutes
x1 = 237 degrees 42 minutes
x2 = 360 degrees - a
x2 = 360 degrees - 57 degrees 42 minutes
x2 = 359 degrees 60 minutes - 57 degrees 42 minutes
x2 = (359 - 57) degrees (60 - 42) minutes
x2 = 302 degrees 18 minutes
This was explanation, how to find a sine x with minus. Now a decision needs to be written down in accordance with bureaucratic rules that I do not know. It looks approximately so.
sin x = -0.8453
x = arcsin (-0.8453)
x1 = 237 degrees 42 minutes
x2 = 302 degrees 17 minutes
Pages
▼
Saturday, September 29, 2012
Thursday, September 13, 2012
Phlogiston theory and complex numbers
At the beginning of XVIII century the theory of phlogiston appeared in chemistry and explained the process of burning the presence of "a fiery substance" to combustibles. It was believed that when the material is burned, it disappears from the phlogiston. For its time it was the most advanced theory, the first theory in the history of chemistry, through which chemicals become a science.
In the development of this theory, there was such a paradox: in chemical experiments on calcination have found that scale weighs more than the metal itself. Instead, that would decrease the mass scale increases when the metal is released phlogiston. Here come to the aid of physics mathematics with its negative numbers. The logic was clear - if there are positive and negative numbers, so there is a positive and negative mass. The theory of phlogiston recorded that phlogiston has negative mass, which is confirmed by experiments - negative weight of phlogiston leaves the metal and enters the air, resulting in a positive mass scale increases.
Thanks to the work of Antoine Lavoisier was digging the role of oxygen in the combustion process and replaced the phlogiston theory came the oxygen theory of combustion. In the new theory, the increase in mass scale was explained in the positive numbers: the weight of the metal added weight of oxygen from the air, resulting in a mass scale increases. That's so simple and effective negative numbers were expelled from chemistry. Because of this, today we enjoy the benefits of chemistry in the form in which they exist.
But physics lurking different fate. Where did the complex numbers? From the same place there was a weight of phlogiston - of negative numbers. This is the common parent of the two theories are even conduct DNA analysis is not necessary. Why is this? To understand this, one must look at the history of mathematics.
In the development of this theory, there was such a paradox: in chemical experiments on calcination have found that scale weighs more than the metal itself. Instead, that would decrease the mass scale increases when the metal is released phlogiston. Here come to the aid of physics mathematics with its negative numbers. The logic was clear - if there are positive and negative numbers, so there is a positive and negative mass. The theory of phlogiston recorded that phlogiston has negative mass, which is confirmed by experiments - negative weight of phlogiston leaves the metal and enters the air, resulting in a positive mass scale increases.
Thanks to the work of Antoine Lavoisier was digging the role of oxygen in the combustion process and replaced the phlogiston theory came the oxygen theory of combustion. In the new theory, the increase in mass scale was explained in the positive numbers: the weight of the metal added weight of oxygen from the air, resulting in a mass scale increases. That's so simple and effective negative numbers were expelled from chemistry. Because of this, today we enjoy the benefits of chemistry in the form in which they exist.
But physics lurking different fate. Where did the complex numbers? From the same place there was a weight of phlogiston - of negative numbers. This is the common parent of the two theories are even conduct DNA analysis is not necessary. Why is this? To understand this, one must look at the history of mathematics.
Wednesday, September 12, 2012
Trigonometry formulas multiple angles



Formulas in trigonometry multiple angles enjoy. There is a sine, cosine, tangent and cotangent double, triple, multiple arguments. In simple words, sin, cos, tg, ctg two alpha, alpha three, four and five alpha.
For all of the double angle formulas are written continuously through equality. In simplifying trigonometric expressions, these formulas taken as read from left to right and right to left in any order. Such a method of making the right formula is called the "method of sewing." Cut a piece of it, there is a piece, sewn together by an equal sign = Get ready-made formula. Cut to full expression, from one of the equal sign to the other. The drafters of the tasks do so. Or something like that then can think of to confuse you more.
Why are these formulas of trigonometry? To simplify trigonometric expressions, which complicated the task compilers. Perhaps they need more in some cases, but it's hard to come up with such. It is necessary to ask the physicists and engineers, whether they had to use these formulas.
Thursday, September 06, 2012
Basic trigonometric identities formula

Basic trigonometric identities of the formula is the basis of trigonometry. First formula circled outline in red wine, called basic trigonometric identities. Actually it is the Pythagorean theorem for trigonometric functions.
Two other formulas identities are obtained if the first equation divided by the square of the cosine of the angle alpha, or the square of the sine of that angle. The last formula is the trigonometric form of the basic properties of all the numbers: if the number is multiplied by the inverse number (or divided by the same number, which is the same thing) the result is a unit.
All the other bells and whistles this trigonometric formulas for basic trigonometric identities and definitions of trigonometric functions. No matter what corner of the universe you are, no matter what with the extraterrestrial civilizations did not communicate, basic trigonometry all be the same. Just do not want to write his formula, trying to prove that you are a human being. For any alien all these equations and symbols the same as that for you Chinese characters. Geometry - that a language that can easily do without interpreters to communicate with any intelligent creature from any planet. Animals are not able to understand the language of geometry. Of course, before you communicate in the language of geometry, it is necessary to learn the language by use.
Where does the basic trigonometric identities? Here's the "Legend of the sine and cosine," in which I explained his version of the occurrence of a trigonometric miracle.
Degree trigonometric functions formula

Degree trigonometric functions formula - very crib in the study of trigonometric functions. Here are the squares, cubes, and fourth-degree sine, cosine, tangent, cotangent. Still, these formulas can be called the degree of reduction formulas of trigonometric functions. In mathematics, like juggling different formulas, the formulas of trigonometry is just for the occasion.
If you take a particular angle, you will find it to trigonometric functions of the formulas, and then substitute these values into the formula and the appropriate calculations, the left and right sides you should get the same. What, in fact, says equality.
Wednesday, September 05, 2012
Matrix in mathematics
Matrix in mathematics perform quite a significant role. With the theory of matrix magic sort it out themselves on your textbooks. I want now to reason about sense of the matrix numbering. Many people know that the matrix used to solve systems of linear equations and matrices used for these purposes. I will not repeat the textbooks, and I suggest you go to kindergarten and there to look for the meaning of mathematical operations with matrices.
So, we will think of the simplest child's task about dogs and cats: "Now in zoosalone 2 cats 3 dogs clipped their wool. While 4 cats and 5 dogs are waiting in the queue. So how many cats and dogs want to change their image?" Simple task on two independent mathematical actions: add up the cats to the cats, add up the dogs to the dogs and get the result two numbers. One of which is the number of the cats, and the second the number of the dogs. That is simply. Now we will solve this task with the use of the matrix numbering on the calculator matrices.
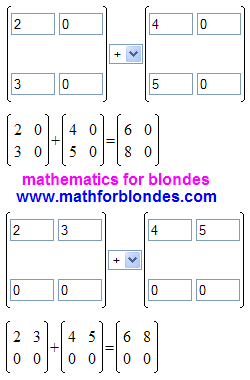
Here's what happened. As creators of calculator consider that operations with row vectors and column vectors are too primitive for mathematical knowledge of such high level, I had to go to a trick. The missing elements of square matrix the second order (this is the minimum size for the calculator matrices) I replaced with zeros.
On a picture it is shown that, I decided this task two methods: first, the values were in the first column, and then I put the same values in the first row of the matrix. Both variants gave the right result. From this we can conclude that the mathematical matrix operations within the meaning of a concurrent execution of mathematical operations with variables that have different units of measure.
In drawing up the matrix to solve a system of linear equations as a unit of measurement to take a unknown. For example, a unit of the decimal number system (just a number, the constant term of the equation), x, y, z, XXL ... Oh! It not from here, this unit is used to measure blouses. By the way, if you write in a matrix the number of your blouses, the matrix of this does not hurt - it does not matter what or where you are writing. But the correct solution to a system of equations with the matrix in the blouse you have not come out.
The principle of a matrix of equations for you take the numerical coefficients before unknown and inscribe them each into the place. That is where the matter of what and where exactly do you fit into the matrix. Then the resulting matrix solving.
Where is yet used principle of mathematical operations with matrices? When you count a whole bunch of money in paper notes and coins. Laid out bills and coins into piles on the dignity and recalculate the number in each pile. On this matrix method ends, farther you bring the got results to a single unit of measurement. Naturally, performing similar actions in everyday life, we never think about how it can be described mathematically.
Remember, we talked about the meters and decimetres? About bows and flounces, on a multi-core processor? There also can be used matrix methods of addition and subtraction. Perform all actions with the same unit of measurement, then all of the other unit of measurement. In the end, if necessary, make conversion between different units of measurement to another.
This method is very good to use in geodesy, when you need to add or subtract a large number of angles in degrees, minutes, seconds. Doing all the actions in degrees, then a minute, then with seconds. And then all received converting seconds into minutes and seconds. To obtain the minute add or subtract those moments obtained after converting seconds. Convert the result to degrees and minutes. To add on the total number of degrees degrees of minutes. All you have turned a corner in degrees, minutes, seconds.
I hope this article will be useful in practice, and you're using methods of matrix computations is in full knowledge of what you are doing and what the result will get.
So, we will think of the simplest child's task about dogs and cats: "Now in zoosalone 2 cats 3 dogs clipped their wool. While 4 cats and 5 dogs are waiting in the queue. So how many cats and dogs want to change their image?" Simple task on two independent mathematical actions: add up the cats to the cats, add up the dogs to the dogs and get the result two numbers. One of which is the number of the cats, and the second the number of the dogs. That is simply. Now we will solve this task with the use of the matrix numbering on the calculator matrices.

Here's what happened. As creators of calculator consider that operations with row vectors and column vectors are too primitive for mathematical knowledge of such high level, I had to go to a trick. The missing elements of square matrix the second order (this is the minimum size for the calculator matrices) I replaced with zeros.
On a picture it is shown that, I decided this task two methods: first, the values were in the first column, and then I put the same values in the first row of the matrix. Both variants gave the right result. From this we can conclude that the mathematical matrix operations within the meaning of a concurrent execution of mathematical operations with variables that have different units of measure.
In drawing up the matrix to solve a system of linear equations as a unit of measurement to take a unknown. For example, a unit of the decimal number system (just a number, the constant term of the equation), x, y, z, XXL ... Oh! It not from here, this unit is used to measure blouses. By the way, if you write in a matrix the number of your blouses, the matrix of this does not hurt - it does not matter what or where you are writing. But the correct solution to a system of equations with the matrix in the blouse you have not come out.
The principle of a matrix of equations for you take the numerical coefficients before unknown and inscribe them each into the place. That is where the matter of what and where exactly do you fit into the matrix. Then the resulting matrix solving.
Where is yet used principle of mathematical operations with matrices? When you count a whole bunch of money in paper notes and coins. Laid out bills and coins into piles on the dignity and recalculate the number in each pile. On this matrix method ends, farther you bring the got results to a single unit of measurement. Naturally, performing similar actions in everyday life, we never think about how it can be described mathematically.
Remember, we talked about the meters and decimetres? About bows and flounces, on a multi-core processor? There also can be used matrix methods of addition and subtraction. Perform all actions with the same unit of measurement, then all of the other unit of measurement. In the end, if necessary, make conversion between different units of measurement to another.
This method is very good to use in geodesy, when you need to add or subtract a large number of angles in degrees, minutes, seconds. Doing all the actions in degrees, then a minute, then with seconds. And then all received converting seconds into minutes and seconds. To obtain the minute add or subtract those moments obtained after converting seconds. Convert the result to degrees and minutes. To add on the total number of degrees degrees of minutes. All you have turned a corner in degrees, minutes, seconds.
I hope this article will be useful in practice, and you're using methods of matrix computations is in full knowledge of what you are doing and what the result will get.