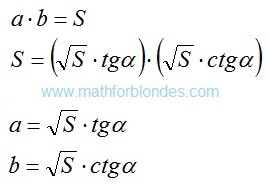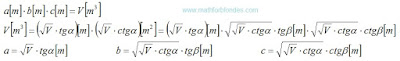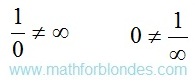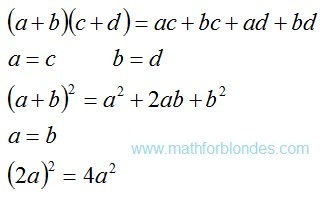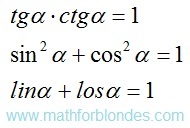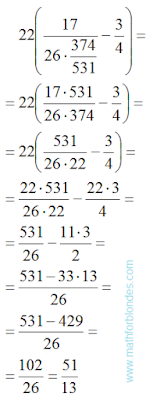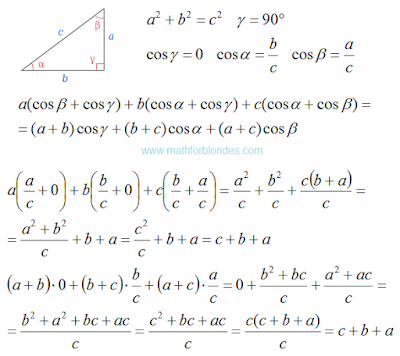The linear angular functions

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Division

Lesson 14

The linear angular functions

If to consider terminating trigonometric functions as coordinates of points of a unit circle in a Cartesian coordinate system, then the linear angular functions are coordinates of points of the chord connecting circle cross points to a coordinate. The sum of coordinates of any point of this chord is always equal to unit.

The linear angular functions

In mathematician of a concept, similar to the linear angular functions, are used since ancient times - it is division whole on a part. In the modern world an analog are percent.

The explanation for readers of this website. For myself I called the linear angular functions "linos" and "loses". How I thought up these names? Took designation of a sine and cosine. Visually they quite well differ. In each designation I replaced the first letter with the Latin letter "l" from the word "line". It turned out quite nicely. But to solve to you. Whether these functions in mathematician will get accustomed and as they will be called - time will show. I just offer one more mathematical tool for the description of reality.

At the following lesson we will consider
Addition

Division

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Decomposition on factors

Lesson 13

Division

Contrary to the standard opinion, division is not mathematical operation. This solution of a standard task of finding of one of factors if other factor and result of multiplication is known. In ancient Babylon the fraction was considered as result of multiplication of number to inverse other number. Even in the modern mathematics there is no division of one fraction into other fraction, this operation is replaced with multiplication of a dividend to fraction, inverse to a divider.

Division can be considered as a projection of result of multiplication along one of factors. For example, length is a projection of the area along width, width is a projection of the area along length.

The most interesting in this plan is the speed which is measured by the lengthiest, divided into time. If to assume that length is result of multiplication of two perpendicular directions of time, then speed is a projection of length (the area of time) along one of the directions of time. For a comprehension of the nature and an essence of light velocity, this approach can be the very useful.

At the following lesson we will consider
The linear angular functions

Decomposition on factors

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Zero and infinity

Lesson 12

Decomposition on factors

Mathematical operation, opposite on sense to multiplication, decomposition on factors is. It is carried out with application of the infinite trigonometric functions.

Decomposition on factors

 The most prime example of decomposition on factors at an angle in 45 degrees is root squaring. As both factors in this case are identical, as result of decomposition it is accepted to write down only one of factors.

Decomposition on factors can be applied when only the result of multiplication is known and any of factors is not known. Units of measure as a result decomposition on factors should be selected intuitively so that as a result of their multiplication the tentative unit of measure turned out. The quantity of spacelike dimensions in units of measure of factors at decomposition can be a miscellaneous. For example, three-dimensional volume can be spread out to one-dimensional factors by means of two operations of decomposition, one of options looks so:

Decomposition of volume

In this example corners α and β are not bound among themselves. If to display volume in a cube (a=b=c), then α≈35° is a angle between the diagonal of a cube and diagonal of the basis, β=45 ° is a angle between the diagonal of the basis and its party.

At the following lesson we will consider
Division

Zero and infinity

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Distinctions between multiplication and addition

Lesson 11

Zero and infinity

If the angle is equal to zero or 90°, then the two dimensional rectangle disappears and there is a one-dimensional piece. From here the sense of infinity follows: as if we did not change the party of a rectangle, it will never turn into a piece. Unit divided into zero is not equal to infinity. Infinitesimal size is not equal to unit divided into infinity.

Zero and infinity

Difference between elements in these inequalities same as difference between the point lying on a straight line and the point which is not lying on a straight line.

Multiplication to zero and division by zero do not fall into to mathematical operations with numbers, they are carried out in the field of units of measure. It is possible to call these values of trigonometric functions non-numerical.

In addition to the materials about multiplication and division by zero explained earlier it is necessary to add the following. In positional notation zero designates lack of number of the particular category. Lack of number number cannot be. Here zero is similar to punctuation marks in writing which have the graphic form, but are not said when reading.

Generally zero should be understood as lack of the considered unit of measure. For example, zero value of a angle means that the angle is absent. Division by zero should be considered as need of introduction of a unit of measure, perpendicular to already existing, for the further solution of a task. Division by zero does not mean automatic transition to multiplication. For example, it is impossible to describe turn of a piece in one-dimensional space, for this purpose it is necessary to enter padding measurement and to consider a task in two dimensional space.

At the following lesson we will consider
Decomposition on factors

Distinctions between multiplication and addition

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Examples of multiplication

Lesson 10

Distinctions between multiplication and addition

Multiplication is a change of quality, that is change of units of measure. Contrary to the standard opinion, multiplication cannot be presented in the form of addition. When multiplication is substituted for addition, mathematical properties of multiplication are used. With units of measure substitution looks so:

Multiplication substitution by addition

Algebraic expressions with use of letters show distinction between addition and multiplication:

Multiplication in algebra

If at addition items have identical numerical values, then it is possible to apply mathematical model of multiplication for addition. At the same time we assume that units of measure at multiplication do not change:

Addition replacement with multiplication

In mathematician possess separate properties of units of measure:

- number systems of numbers – it is impossible to addition the numbers presented in different number systems, a question of a possibility of multiplication of numbers in different number systems the author it was not studied;

- denominators of common fractions – it is impossible to addition fractions with different denominators, at multiplication of fractions denominators are multiplied;

- alphabetic references in algebraic expressions – it is impossible to addition numbers with different designations, at multiplication new designation of result turns out;

- legends of functions (for example, trigonometrical).

At the following lesson we will consider
Zero and infinity

Examples of multiplication

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Multiplication

Lesson 9

Examples of multiplication

Multiplication in space

At interaction of two one-dimensional spaces (in figure D is quantity of spacelike dimensions) the two dimensional space turns out. At addition to interaction of perpendicular measurement, the quantity of spacelike dimensions of result increases. It is necessary to understand any quantities participating in multiplication as spacelike dimensions. Multiplication of two one-dimensional lengths gives the two dimensional area, multiplication of the two dimensional area at one-dimensional length gives three-dimensional volume and so on. The possibility of receiving four-dimensional space as a result of multiplication of two two dimensional spaces is theoretically possible, but demands specification from the point of view of physical reality.

Examples of multiplication

Voltage is result of interaction of current intensity and resistance. If to consider current intensity not as one-dimensional quantity and as two dimensional (the area of current), then as a result of interaction with a resistance power will turn out. Units of measure of the specified quantities (Volts, Ampere, Ohms, Watts) are household (convenient in daily use), but demand mathematical representation for comprehension of an essence of the physical processes expressed by these units of measure. The system of physical quantities offered R.O. di Bartini can be considered as attempt of transition from household units of measure to mathematical. Interaction between quantities is carried out due to the processes studied in physics.

The arrangement of threads in the perpendicular direction allows to receive cloth. Interaction between threads is carried out at the expense of frictional force. If in the perpendicular directions to arrange reinforcing rod stock, then it is possible to receive a two dimensional reinforcing grid or a three-dimensional reinforcing framework. Interaction of separate rod stock in clusters is provided with electric welding or a knitting wire. Plywood is the fibers of a wood neveer located perpendicularly. Interaction is provided by pasting of separate layers of wood neveer.

At multiplication the quantity of goods on unit price, as a result turns out the cost of a consignment of goods (sum). It is an example of application of mathematical model of multiplication to the virtual units of measure. In this case physical interaction between goods and the price is absent.

Sexual reproduction it is possible to present in multiplication form. As a result of interaction of a male and a female there is a posterity which has genetic signs of two parents. Partial transfer of genetic signs from each of parents can be described by means of the linear angular functions.

For more precise reflection of reality in mathematician it is necessary to consider three stages of multiplication: beginning of multiplication, interaction process, end of multiplication. In electric circuits the switch is the device which operates interaction. Creation of cloth, plywood, a reinforcing grid is the beginning of interaction. Physical destruction of these objects is the end of interaction.

At the following lesson we will consider
Distinctions between multiplication and addition

Multiplication

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Variable units of measure

Lesson 8

Multiplication

As a result of multiplication of two different quantities the third quantity turns out. At multiplication of change occurs both in a number domain, and in the field of units of measure. Multiplication is possible only for perpendicular quantities. Multiplication reflects high-quality changes of quantities.

Multiplication of the parties of a rectangle allows to receive the area.

Multiplication of the parties of a rectangle

For transition from the area of a rectangle to the simple area it is necessary to divide the square into itself. In this case two options of algebraic transformations are possible. It is necessary to highlight that the recommendation of mathematicians about reduction of identical quantities in numerator and a denominator of fraction is consciously controlled for identification of quantity of the received result. The first option of transformations looks as follows.

First option of the unit area

The tangent and cotangent are connected by the inverse proportion. The parties of a rectangle can change somehow, from infinitely big quantity to infinitesimal. If change of the parties is carried out with keeping of the inverse proportion, then the area of a rectangle will remain invariable.

The second option of transformations is presented in an algebraic form and in physical units of measure.

Second option of the unit area

This transformation shows that as a result of multiplication of two different units the third unit turns out. Multiplication is an interaction of two perpendicular units of measure as a result of which the new unit of measure turns out. As any quantity is result of multiplication of number and a unit of measure, under figure "one" can the number, a unit of measure or result of their interaction is meant.

Perpendicular units of measure are not connected among themselves in any way and can have the arbitrariest scale. The scale of units of measure of factors scales work units of measure, but does not influence a process essence – multiplication leads to high-quality change of initial units of measure.

The area is a result of interaction of two perpendicular measurements of length. If to multiplication inches by meters or millimeters on meters, then the area will be expressed in inches on meter or millimeters on meter. Traditionally, the area can be expressed in identical units of measure of length and width. In practice frames with different scales on a vertical and a horizontal are often used.

At determination of the area of a square the size of the party can be built in the second degree. But it does not mean at all that the party of a square is multiplied by itself. The area can still be determined only by multiplication of length to width, just at a square they have identical numerical values. We never multiply rectangle length by length or width on width because the result of such actions does not make sense. The involution is a multiplication of the different perpendicular quantities having identical numerical values and units of measure.

Algebraic transformations of multiplication of two to a square can be written down so:

Algebraic transformations

If to consider that quantity a at a quadrating is multiplied by itself, then the inverse transformation of a square in work of two sums will be impossible. As it is possible to execute a similitude, is shown in the partition Decomposition of sume below.

Diagonal of a rectangle and angle between the diagonal and the party are padding characteristics of the interacting quantities.

At the following lesson we will consider
Examples of multiplication

Variable units of measure

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Quantity

Lesson 7

Variable units of measure

Example of variable units of measure are exchange rates of the different countries. The main world currencies are in continuous fluctuation. They are connected by laws of the inverse symmetry – rise in price of one currency means reduction in cost of other currency.

One more example. Why people never celebrate such significant day how "The Middle of Life"? Because nobody knows the precise duration of characteristic life. After death such important parameter as "life expectancy", ceases to change. Similar indeterminacy is characteristic of all living beings.

If to take duration of existence of an alive organism for unit, then the description in variable units of measure will be the most precise mathematical description of any life. As the beginning of this unit of measure it is necessary to consider the conception moment (at sexual manifolding), the end is the death. It is necessary to notice that increase in life expectancy of concrete organisms is not a priority in natural selection.

Quantity, the back symmetric life expectancy, the age is. The age allows to express the variable characterizing life in constant units of measure of time.

From the point of view of mathematics, emergence of life can be considered as transition from constant units of measure (inanimate nature) to variables (wildlife).

At the following lesson we will consider
Multiplication

Quantity

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
The infinite trigonometric functions

Lesson 6

Quantity

Tangent and cotangent

Mathematical interpretation of the drawing given above will look as follows.

Quantity

Both options of representation of quantity are absolutely equal and yield identical result. On a numerical axis the parity of numbers and units of measure looks so.

Numbers on a straight line

In this case zero and unit divided into zero act as the horizons which cannot be reached by means of numbers. For further transformation of quantity to a look habitual to us, to the abstract mathematical concepts it is necessary to enter homocentrism elements.

If we consider that across units of measure settle down, and numbers are perpendicular them, then quantity will have two options of representation.

Two options of quantity

The numerical axis takes the following form.

Numerical axis with units of measure

Introduction of the following element of a homocentrism allows to pass to habitual representation of quantity. If we consider that the unit of measure always remains to a constant, then for the adequate description of quantity it is necessary to enter inverse numbers. The inverse symmetry of numbers is result of transition from variable units of measure to constants.

Quantity in constant units of measure

The numerical axis will be transformed as follows.

Numbers and inverse numbers

In this case the numerical axis is represented without imposing of a reflecting symmetry. Unit acts as a point of the inverse symmetry. By the inverse symmetry numbers and units of measure in any quantity are connected. At invariable quantity, decrease of number leads to increase in a unit of measure, increase in number – to decrease of a unit of measure. The algebra of similitudes looks so.

Decrease of number Increase in number

Here elements, the falling into number domains, are represented in round brackets. Elements, the falling into areas of units of measure, are represented in square brackets.

At the following lesson we will consider
Variable units of measure

The infinite trigonometric functions

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Terminating trigonometric functions

Lesson 5

THE INFINITE TRIGONOMETRIC FUNCTIONS

If to divide rectangle elements with simple diagonal into terminating trigonometric functions, the infinite trigonometric functions will turn out.

Transition from terminating trigonometric functions to the infinite

The tangent and cotangent can be presented as the party of a rectangle when as a unit of measure of length length of the perpendicular party is accepted. This geometrical representation of a tangent and cotangent can be considered as visual display of interaction between numbers (the infinite trigonometric functions) and units of measure (unit) as a result of which size appears. Other option of geometrical representation of size is shown in earlier published work.

The tangent and cotangent

Similar representation of numbers and units of measure possesses property of a rectangular symmetry. Value of a angle the alpha in this case characterizes a dependence angle between number and a unit of measure.

At the following lesson we will consider
Quantity

Terminating trigonometric functions

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Three main types of trigonometric functions

Lesson 4

TERMINATING TRIGONOMETRIC FUNCTIONS

The sine and cosine are rather well studied, their values cannot be more unit. If to divide elements of a rectangle into length of diagonal, lengths of the parties will accept values of a sine and a cosine. Also the parties of a rectangle are diagonal projections in the perpendicular directions.

Sine and cosine

Names of all trigonometric functions depend on the line of the beginning of measurement of a angle. The same line defines the direction of projection. Dependence between legs and a hypotenuse in a rectangular triangle, known as "Pythagorean theorem" (for length units of measure, not the bound to a hypotenuse) or "Pythagorean trigonometric identity" (when hypotenuse length is accepted to a unit of measure of length), is an integral part of properties of a rectangle.

If we project simple diagonal on the parties of a rectangle, then we will receive two projections of diagonal expressed through different angles. If we project the same parties on diagonal, then we will receive the diagonal length as the sum of two projections of the parties.

Pythagorean trigonometric identity

The Pythagorean theorem is a dependence between diagonals and the parties of a rectangle.

At the following lesson we will consider
The infinite trigonometric functions

Three main types of trigonometric functions

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Angular symmetry in a rectangle

Lesson 3

Three main types of trigonometric functions

Trigonometric functions are the dependences between angles and numbers in a rectangle expressed in own units of measure. Own unit of measure is one of characteristics of object, accepted as a unit of measure.

In a rectangle it is possible to allocate three main types of trigonometric functions:

- the infinite trigonometric functions – a tangent and a cotangent, geometrically it:

a) the size of one of the parties of a rectangle at simple value of length of other party, is reflected by communication of numbers and units of measure;

b) the sizes of the parties of a rectangle at simple area, reflect laws for multiplication;

- terminating trigonometric functions – the sine and a cosine, geometrically are the sizes of the parties of a rectangle at simple diagonal, reflect projective properties of space;

- the linear angular functions – the linear sine (lin) and the linear cosine (los), geometrically is the sizes of the parties of a rectangle at a simple semiperimeter, reflect laws of addition.

Other types of trigonometric functions in this work are not considered as they did not draw attention of the author. All trigonometric functions establish particular connection between angles and numbers. It is quite possible that the mathematics of some extraterrestrial civilizations can be constructed on angles in the same way as at us it is constructed on numbers.

Expression of the trial trigonometric functions through the parties of a rectangle.

Expression of the trial trigonometric functions through the parties of a rectangle

The main ratios on types of trigonometric functions.

The main ratios on types of trigonometric functions

Values of trigonometric functions of some angles.

Values of trigonometric functions of some angles

Expression of one trigonometric functions through others.

Expression of one trigonometric functions through others

The explanation for visitors of this website. If to look at formulas of a tangent and a cotangent (the last picture), then can seem that between a sine with a cosine and linos with loses there is no difference. But you do not hurry with conclusions. If two fractions are equal, it does not mean at all that their numerators and denominators are equal. Let's review an example. Two thirds are equal to four sixth. But two it is not equal to four, three it is not equal to six.

In more detail the trial trigonometric functions are considered below.

At the following lesson we will consider
Terminating trigonometric functions

Triangle and rectangle

Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
At the first lesson we saw off
Short analysis of trigonometric functions

Lesson 2

Transformations of a triangle to a rectangle

If to combine two rectangular triangles on diagonal so that the rectangle turned out, then the hypotenuse of a triangle will turn into rectangle diagonal, and the parties of a triangle will turn into the parties of a rectangle. The trigonometrical relations of a triangle turn into the trigonometrical relations of a rectangle.

Transformations of a triangle to a rectangle

Angular symmetry in a rectangle

Diagonal of a rectangle divides a right angle into two trigonometrical angles. The name of a trigonometric function depends on what angle we will take for definition of its numerical value. At the same time the numerical result does not depend on our choice.

Angular symmetry in a rectangle

Names of trigonometric functions and the name of angles possess properties of an angular symmetry. At the same time a symmetry of AND functions of angles are inseparably linked among themselves. If we take the symmetric function and the symmetric angle, then the result will remain invariable. We apply an angular symmetry twice. The similar situation turns out in a plane geometry. If twice to apply a reflecting symmetry, then nothing will change. In algebra analog of an angular and reflecting symmetry is multiplication to minus unit. If an algebraic expression to increase unit by minus twice, the algebraic expression will remain the same.

Reflecting symmetry, the inverse symmetry, angular symmetry, multiplication to minus unit are manifestations of the same law of a symmetry under different conditions.

Considering a symmetry of trigonometric functions, they can be united pairwise in separate groups, each of which expresses particular type of dependence between angles and numbers.

At the following lesson we will consider
Three main types of trigonometric functions

Trigonometric functions in a rectangle

Published on 7 July, 2016
"The Papers of Independent Authors"
Volume 36 of p. 46-69

Annotation

Representation of trigonometric functions in a rectangle allows to unite algebra, geometry and physics in a single whole.

Short analysis of trigonometric functions

Usually trigonometric functions of plane angle are defined in a rectangular triangle as ratios of the parties of this triangle [a reference to the source in the printing edition].

Trigonometric functions in a triangle

If to accept the definitions of trigonometric functions entered by mathematicians in a rectangular triangle, then values of these functions depend only on a ratio of the sizes of the parties of a triangle. The size of angles in a rectangular triangle is in the range of trigonometrical angles. Trigonometric functions have no signs and do not possess periodic. These properties are homocentrism elements.

The homocentrism mathematics is a mathematics in which the result depends on the option of the relative mathematics accepted by us or on our opinion. Striking examples of a homocentrism in mathematician are: division of numbers on positive and the negative, decimal numeration, numbers and inverse numbers, Cartesian coordinate system, etc.

In Cartesian coordinate system trigonometric functions are defined as coordinates of points of a unit circle [a reference to the source in the printing edition].

Trigonometric functions in Cartesian coordinate system

This definition is possible only because for any point of a circle of coordinate are used as padding elements for creation of a rectangular triangle. For cross points of a circle and coordinate creation of a triangle is impossible.

For any point of the plane in Cartesian coordinate system trigonometric functions can be defined as the relation of coordinates of this point or the relation of coordinates of a point to distance from a point to the center of a frame. An exception is the cross point of coordinate (the center of a frame) for which trigonometric functions cannot be defined. This fact is congenital defect of Cartesian coordinate system. If it is necessary to define trigonometric functions for the point coinciding with the center of a frame, then the frame needs to be displaced aside.

In Cartesian coordinate system trigonometric functions are the relative and depend on the relative positioning of the plane on which the considered points, and frames are located. Periodicity of trigonometric functions is result of rotation of a piece around the center of a frame. Signs of trigonometric functions depend on the positive direction of coordinate accepted by us. All this result homocentrism of views of trigonometric functions.

Signs of trigonometric functions "+" and "-" serve for orientation in space of Cartesian coordinate system. In mathematical formulas with use of trigonometric functions, the sign "minus" at function automatically changes addition for a subtraction or a subtraction on addition. In formulas it is possible to do without the negative values of trigonometric functions. It will allow to reduce twice amount of values of trigonometric functions, but will increase quantity of formulas.

At the following lesson we will consider
Transformations of a triangle to a rectangle

More interesting math ideas on the page "My Math"

Measurement of plane angles

Published on 7 July, 2016
"The Papers of Independent Authors"
Volume 36 of p. 43-45

Annotation

Plane angles need to be divided into trigonometrical angles and rotation angles.

Measurement of angles in a solid geometry

In a solid geometry «angle between a straight line and the plane is called angle between this line and its projection (orthogonal) to the plane. If the straight line to be a perpendicular plane, then angle between it and the plane is considered (my italic type – Nikolaj Khizhnjak) equal 90°, and between a parallel straight line and the plane – equal 0°". [1, p. 308].

As appears from definition, the angle between a straight line and the plane cannot be more than 90°. Angles more than 90° fall into to angles of rotation [2, p. 81]. In a solid geometry it is not accepted to describe by means of angles rotation of a straight line around a point of its crossing with the plane.

If the straight line is parallel to the plane (or belongs to the plane), then it is considered, that the size of the angle has zero value. Actually there is no vertex of angle – a cross point of a straight line and the plane. If the perpendicular plane straight line, then a trace turns into a point which coincides with a cross point of a straight line and the plane. Actually there is no second ray forming a angle. In this case the angle is considered right angle.

Measurement of angles in a planimetrics

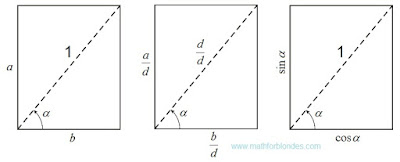
On analogies to a solid geometry, a plane angle between two straight lines (line segments) it has to be measured as a angle between a point on one direct and its projection on other straight line with vertex of angle in a cross point of these straight lines.

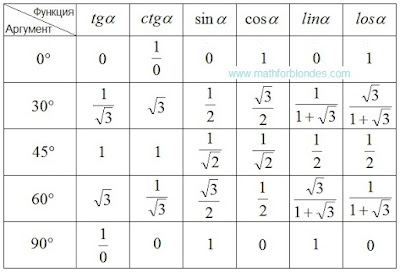
This rule allows to divide plane angle into trigonometrical angles (from 0° to 90°) and rotation angles. The fundamental difference between these angles consists in amount of the objects on the two dimensional plane forming a angle. The trigonometrical angle is measured between two different objects, the rotation angle is measured between two provisions (initial and terminating) one object. For trigonometrical angles the time factor is absent, for rotation angles the time factor is obligatory: tentative situation, rotation time, terminating situation.

At measurement of angles between two parallel straight lines the angle cannot be defined because there is no cross point of straight lines. At measurement of a corner between two perpendicular straight lines the angle cannot also be defined because the projection of a point coincides with a cross point of these straight lines.

Conclusion: zero and right angles cannot have just the same mathematical properties as other angles. In more detail these distinctions will be described by consideration of trigonometric functions.

Angles and distances

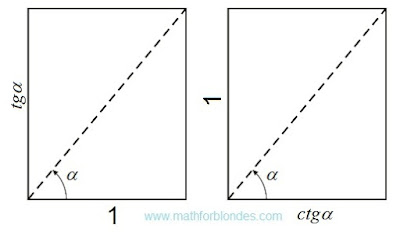
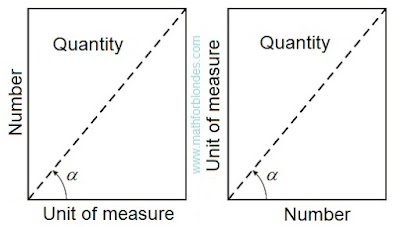
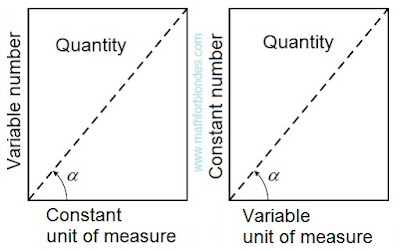
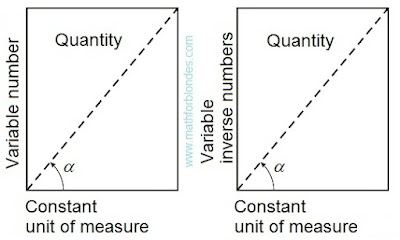
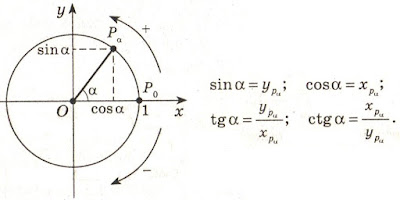
The trigonometrical angle on the properties is similar to distance between two points, the rotation angle is similar to the passable way between the same points. If driving is carried out in a straight line, then the passable path is equal to distance between initial and terminating points of a way. If rotation is carried out on a angle to 90°, then the angle of rotation is equal to a trigonometrical angle. The rotation angle cannot be less trigonometrical angle, the passable path cannot be less than a distance between points of the beginning and end of this way. The distance between two points can be in the numerical range from zero ad infinitum. Compliance between angles from 0° to 90° and numbers from zero ad infinitum is established by a trigonometric function of a tangent of these angles.

The passable path is also expressed in the numerical range from zero ad infinitum even if the distance between an initial and finishing point of the passable way is equal to zero. In the same way the rotation angle can reach infinitely great values, at the same time the trigonometrical angle between the beginning and the end of rotation can be equal to zero. In this case it is possible to establish direct analogy between number and size of a angle as it is accepted in a calculus.

Various mathematical tools, for example, a Pythagorean theorem are used to calculation of distance between initial and terminating points of the passable path. Reduction formulas of angles are applied to definition of a angle between the beginning and the end of rotation.

Conclusion: plane angle on the properties are similar to distances on the plane.

Literature

1. Zabelyshynskaia M.Y."Mathematician. Educational and practical reference book" Kharkiv, Ranock, 2010.
2. Khizhnjak Nikolaj «Bases of mathematics», The Papers of Independent Authors, vol. 19, 2011.

P.S. This article is published for a warming up. Article about trigonometric functions in a rectangle will be a headliner of new work. I hope, from it you learn a lot of new and interesting.

The equation a fraction

What if the equation of lead shot, and X is hidden in the denominator? We need to get rid of the denominator. What will happen with X? Do not worry. If you do everything correctly, he from the denominator goes into the numerator. Here you can recommend two ways to solve the equation.

The first method is to bring the expression to normal proportions. Then we use the proportion of the property - the multiplication of extreme terms in proportion equal to the multiplication of the average proportion of members. Denominator magically disappear. We get a simple equation, which can be easily solved. Consider an example.

The equation a fraction

The number did not work nicely. Make checks and look at the result. Substitute the original expression instead of X its value.

Checking equation

The audit showed that the equation is solved correctly.

The second method is to bring the expression to a common denominator. The denominator should be common to the left and right sides of the equation. In this case, we in good conscience can throw the denominator in the trash. We see an example of reduction to a common denominator.

The equation a fraction

The result was the same as in the first case.

Law of cosines in general

To present the law of cosines in general need to go back to the beginning. If the expression for one side of the triangle the length multiplied by the same hand n-times, the equation does not change.

Conversion formulas

If you add equal to three sides of the triangle, we obtain the law of cosines in general.

Law of cosines in general

The law of cosines in general terms describes the relationship between the sides and angles of a triangle in a multidimensional space. If the given equation is satisfied, then the triangle is in the Euclidean space. Options description triangle in curvilinear spaces require further study. For the correct application of the law of cosines in solid geometry, spherical triangles side length should be unit of measurement in the same units of measurement, which is measured in planimetrics.

Degenerate triangle

Finally, we will check the law of cosines to the perimeter in the degenerate triangle. There can be two options. If we decrease the base of an isosceles triangle to zero, we obtain the two overlapping segments. The sum of the angles of this degenerate triangle is 180 degrees.

Degenerate triangle

If we combine the upper vertex of the triangle with the base, we get the second type of degenerate triangles. This segment equal to the sum of the other two segments. The sum of the angles are also equal to 180 degrees.

Degenerate triangle

A degenerate triangle - is the lower limit of the application of the law of cosines. After that we will look at the law of cosines in general.

Isosceles obtuse triangle

Now we will check how the law of cosines in obtuse triangle. For example, consider an isosceles obtuse triangle.

Isosceles obtuse triangle

Ups! The perimeter of the triangle may be square roots. The law of cosines is not working? Do not jump to conclusions. The secret is revealed very simple. Let us express the base of the triangle through the sides and see what happens. Double-paste the resulting equation in our result. First time turvy-topsy, second time topsy-turvy.

The perimeter of the triangle

The law of cosines to the perimeter works flawlessly. We have completed our review of the degenerate triangle.

Right triangle

Now we will check the law of cosines to the perimeter of the example of a right triangle. At one corner of the right triangle is 90 degrees, the cosine of this angle is zero. Cosine of the other angles are obtained by dividing the length of the hypotenuse to the length of the adjacent side. In general, the law of cosines check looks like.

Right triangle

Now we substitute in formula for the length of the sides of a right triangle and values of cosines.

Right triangle

These values are equal to the perimeter of the triangle. Cosine law allows to check the triangle on the break. That's what happens when one of the sides does not reach the top of the triangle.

Broken triangle

Equality is performed, but the result is not equal to the sum of the lengths of a broken line or the perimeter of the triangle. You can then proceed to test the law of cosines in the isosceles obtuse triangle.

Check the law of cosines

Check the law of cosines for the perimeter, we start with an equilateral triangle. All sides of an equilateral triangle are equal. All angles are equal to 60 degrees. The perimeter of the triangle is equal to three times the length of the sides.

Equilateral triangle

Equality is performed. Now we check the law of cosines in a right triangle.

Law of cosines for perimeter

Carefully look at the proof of the law of cosines and make some corrections.

Analysis of proof

Now we can write the law of cosines for the perimeter of the triangle.

Law of cosines for perimeter

The result is a very simple and beautiful formula that describes the entire triangle. The law of cosines shows a relationship between the angles and the lengths of the sides of a triangle.

The geometry of the law of cosines

Law of cosines for perimeter describes the perimeter of the triangle made up of one-dimensional Euclidean spaces. For multidimensional spaces cosine law has a different view.