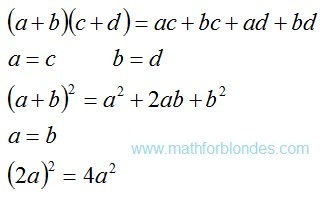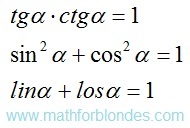Subject of occupations:
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Distinctions between multiplication and addition
Lesson 11
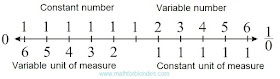
Zero and infinity
TRIGONOMETRIC FUNCTIONS IN A RECTANGLE
Subject of the previous lesson
Distinctions between multiplication and addition
Lesson 11
Zero and infinity
If the angle is equal to zero or 90°, then the two dimensional rectangle disappears and there is a one-dimensional piece. From here the sense of infinity follows: as if we did not change the party of a rectangle, it will never turn into a piece. Unit divided into zero is not equal to infinity. Infinitesimal size is not equal to unit divided into infinity.
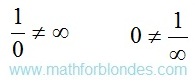 |
| Zero and infinity |
Difference between elements in these inequalities same as difference between the point lying on a straight line and the point which is not lying on a straight line.
Multiplication to zero and division by zero do not fall into to mathematical operations with numbers, they are carried out in the field of units of measure. It is possible to call these values of trigonometric functions non-numerical.
In addition to the materials about multiplication and division by zero explained earlier it is necessary to add the following. In positional notation zero designates lack of number of the particular category. Lack of number number cannot be. Here zero is similar to punctuation marks in writing which have the graphic form, but are not said when reading.
Generally zero should be understood as lack of the considered unit of measure. For example, zero value of a angle means that the angle is absent. Division by zero should be considered as need of introduction of a unit of measure, perpendicular to already existing, for the further solution of a task. Division by zero does not mean automatic transition to multiplication. For example, it is impossible to describe turn of a piece in one-dimensional space, for this purpose it is necessary to enter padding measurement and to consider a task in two dimensional space.
At the following lesson we will consider
Decomposition on factors
Decomposition on factors