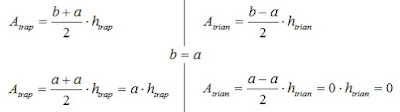In Wikipedia there is a page of a trapezoid. In the drawing it is shown that any trapezoid can be turned into a rectangle.
 |
| Trapezoid |
Let's look at algebra. These are formulas for calculation of lengths of diagonals of a trapezoid.
 |
| Diagonals of trapezoid |
We substitute in these formulas data for a rectangle.
 |
| Diagonals of rectangle |
If to trust these formulas, the rectangle has no diagonals. Even schoolboys or schoolgirls can make what mathematicians couldn't make – to execute verification of the solution of a task. It is the actual level of modern mathematics – any statement of mathematicians can be false.
Height of a trapezoid
Height of a trapezoid is determined by the area of a triangle. The area of a triangle is calculated on Heron's formula. The sizes of the parties of a trapezoid allow to receive a triangle which has the same height as a trapezjid. The cunning trick of mathematicians allows to calculate length of diagonals of a trapezoid.
 |
| Height of a trapezoid |
When the legs of a trapezoid are parallel, the triangle disappears and the cunning trick ceases to work. If to determine height of a trapezoid by the area of a trapezoid, then no problems arise upon transition to a rectangle or a parallelogram.
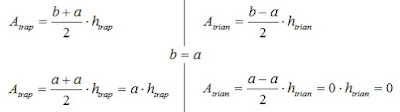 |
| Height of a rectangle |
Conclusion: cunning tricks of mathematicians can lead in false results.
More interesting math ideas on the page "My Math"